1)Նշիր նկարին համապատասխան պնդումները:

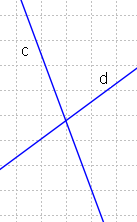
Այս ուղիղները`

• հատվում են
• զուգահեռ են

2․Եթե հարթության վրա երկու ուղիղներ զուգահեռ են, ապա այդ ուղիղները չեն հատվում:

• ճիշտ է
• սխալ է

3․Ճիշտ է արդյո՞ք հետևյալ պնդումը`AB∥ IE:

Այս ուղիղները իրար զուգահեռ են, քանի որ ուղիղները համապատասխան են և ունեն հավասար անկյուններ։

4․c ուղիղը հատում է a և b ուղիղները: Գտիր այնպիսի անկյուն, որը ∠4-ի հետ կազմի միակողմանի անկյունների զույգ:

∠4-ի հետ 7-ը կկազմի միակողմանի անկյունների զույգ։

5.ABC անկյունը 65⁰ է, իսկ BCD անկյունը՝ 115⁰։ AB և CD ուղիղները կարո՞ղ են, արդյոք, լինել՝

ա)զուգահեռ են, եթե BC-ն AD-ի մի կողմում է      բ)հատվող

6.Գծիր ABC եռանկյունը և տար ED∥AC հատվածները: Հայտնի է, ր՝ D∈AB,E∈BC, ∢CBA=77°,∢BDE=55°

180-132=48°

Գտիր∡BCA։

∡BCA=48°, քանի որ DEB և ABC-ն համապատասխան են, և զուգահեռ։

7․Երկու զուգահեռ ուղիղներ երրորդով հատելիս առաջացած խաչադիր անկյունների գումարը հավասար է 210⁰ ։Գտնել այդ անկլյունները։

Քանի որ խաչադիր անկյունները իրար հավասար են, ապա՝․ 210։2=105⁰ յուրաքանչյուր անկյունը։

8․ Երկու զուգահեռ ուղիղներ երրորդով հատելիս առաջացած միակողմանի անկյուններից մեկը 46⁰-ով մեծ է մյուսից։ Գտնել այդ անկյունները։

180-46=134⁰

134:2=67⁰ (անկյուն 1)

67+46=113⁰ (անկյուն 2)

9․BK հատվածը ABC եռանկյան կիսորդ է։ K կետով տարված է ուղիղ, որը BC կողմը հատում է M կետում այնպես, որ BM=MK: Ապացուցել, որ KM||AB:

BM=MK

<1=<2

BKM-ն հավասարասրուն է

<2=BKM

<1=<2=<1=<BKM